موردپژوهی
موردپژوهی به عنوان یک روش تحقیق در روانشناسی، به ویژه در روانکاوی، می‌تواند به ما در درک عمیق‌تری از رفتارهای انسانی کمک کند.
ضریب همبستگی تاوکندال
ضریب همبستگی تاکندال که به افتخار آماردان مشهور ویلیام تاوکندال نامگذاری شده است، معیاری برای سنجش وابستگی آماری بین دو متغیر است. 📈 بر خلاف برخی دیگر از ضرایب همبستگی، تاو تاوکندال یک اندازه گیری ناپارامتریک است، به این معنی که توزیع خاصی را برای داده ها در نظر نمی گیرد.
ضریب همبستگی اسپیرمن
ضریب همبستگی اسپیرمن که به نام چارلز اسپیرمن نامگذاری شده است، یک اندازه گیری آماری است که قدرت و جهت یک رابطه یکنواخت بین دو متغیر رتبه بندی شده را بررسی می کند. برخلاف ضریب همبستگی پیرسون که روابط خطی بین متغیرها را اندازه گیری می کند، همبستگی اسپیرمن رابطه بین متغیرها را زمانی ارزیابی می کند که داده ها ممکن است مفروضات نرمال بودن یا خطی بودن را برآورده نکنند. در این بحث به مفهوم ضریب همبستگی اسپیرمن، محاسبه، تفسیر، کاربردها، مزایا و محدودیت‌های آن خواهیم پرداخت.
همبستگی پیرسون
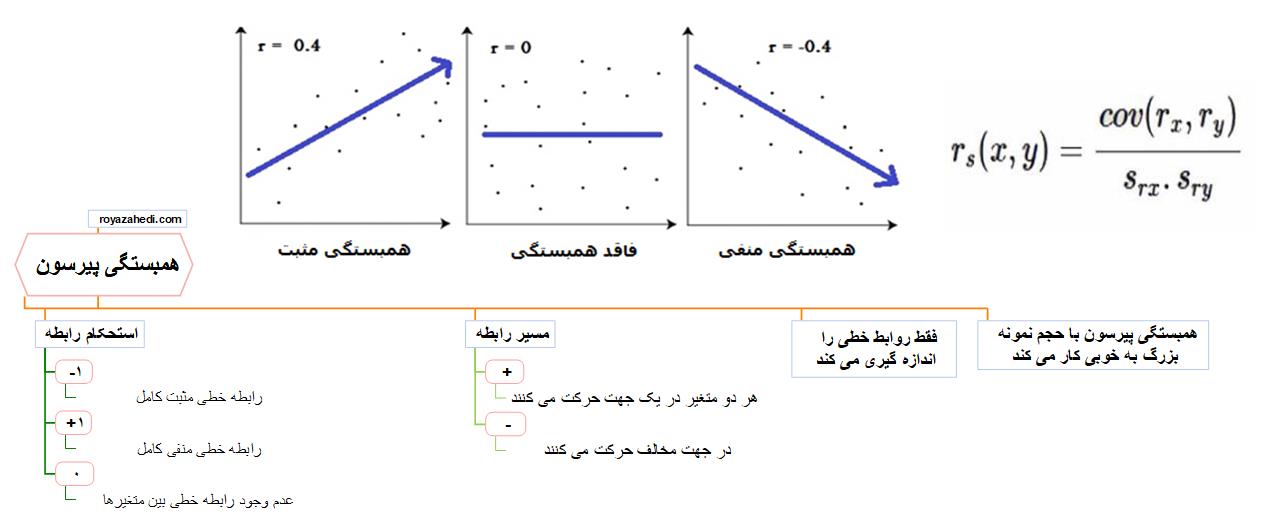
همبستگی پیرسون یک معیار آماری است که میزان رابطه خطی بین دو متغیر پیوسته را کمی می کند. نام آن از کارل پیرسون گرفته شده است که این روش را در اواخر قرن نوزدهم به عنوان راهی برای خلاصه کردن قدرت و جهت یک رابطه خطی بین دو متغیر توسعه داد.
همبستگی در آمار: درک روابط بین متغیرها
در قلمرو آمار، همبستگی به یک معیار آماری اطلاق می شود که قدرت و جهت رابطه بین دو متغیر را توصیف می کند. این به ما کمک می کند تا بفهمیم که چگونه تغییرات در یک متغیر با تغییرات در متغیر دیگر مرتبط است. درک همبستگی در زمینه های مختلف مانند علوم اجتماعی، اقتصاد، روانشناسی، …
