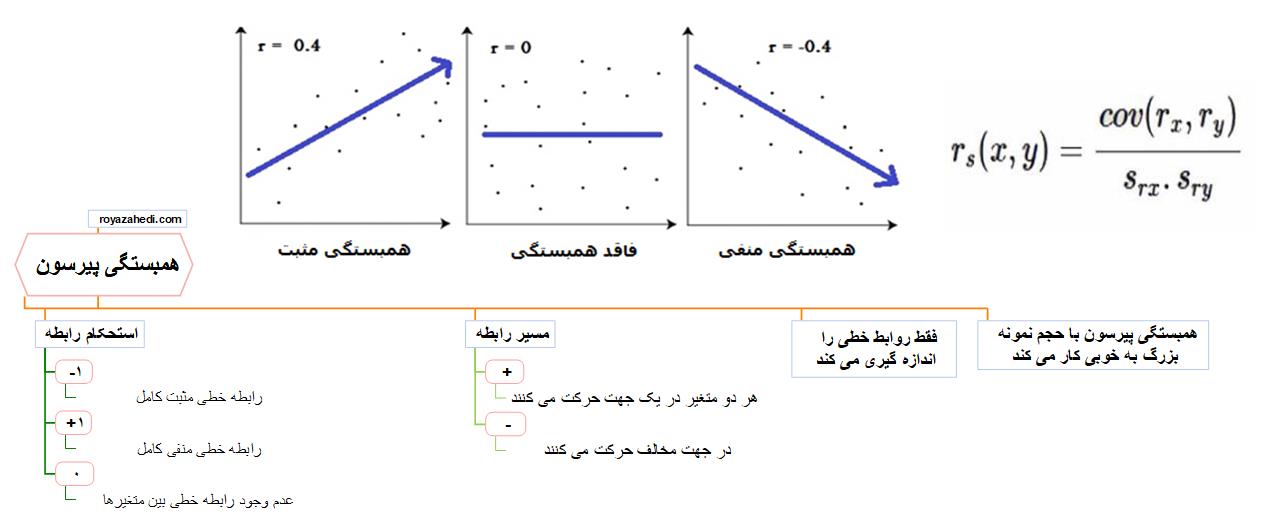
همبستگی پیرسون
همبستگی پیرسون یک معیار آماری است که میزان رابطه خطی بین دو متغیر پیوسته را کمی می کند. نام آن از کارل پیرسون گرفته شده است که این روش را در اواخر قرن نوزدهم به عنوان راهی برای خلاصه کردن قدرت و جهت یک رابطه خطی بین دو متغیر توسعه داد.